De opleiding bachelor in het Vastgoed/Landmeten organiseert 4 workshops landmeten voor leerlingen uit het zesde jaar. Deze workshops duren 3 uur en kunnen worden gevolgd in de maanden oktober en november, februari, maart, april en mei. Datum en grootte van groepen wordt in overleg bepaald.
Doelgroep: zesdejaars secundair onderwijs
Maximaal 20 leerlingen per workshop
Locatie: AP Hogeschool campus Spoor Noord - Ellermanstraat
Wil je graag meer weten of heb je interesse? Mail naar landmeten@ap.be.
Andere workshops:
Deze workshop focust op het aspect van de altimetrie (hoogtemeting) en de uitvoering van een horizontale waterpassing met een waterpasinstrument.
Duurtijd: 3u
Om nieuwe bouwprojecten op een correcte wijze in te passen en wateroverlast te vermijden, zal het noodzakelijk zijn om hoogtemetingen te verrichten. Die hoogtemetingen kunnen uitgevoerd worden ten opzichte van een lokaal referentiepunt of in het nationaal referentiestelsel, nl. het TAW-stelsel (Tweede Algemene Waterpassing).
De hoogtemetingen kunnen variëren van eenvoudige metingen met een verticaal gehouden vouwmeter tot gecompliceerde metingen waarbij, met behulp van een theodoliet, hoeken en afstanden moeten worden gemeten of berekend. Ook bijzondere metingen, zoals dieptemetingen en peilingen met sonar of radar van waterlopen, zandwinningplassen enz. ten opzichte van de waterspiegel vallen onder hoogtemetingen.
Voor landmeetkundige toepassingen wordt de Z-coördinaat meestal bepaald door:
• Trigonometrische hoogtemeting
of
• Horizontale waterpassing
De deelnemers leren de basisbeginselen van de horizontale waterpassing en gaan effectief aan de slag met een waterpasinstrument om deze techniek in de praktijk toe te passen.
Een waterpasinstrument is een optisch instrument waarmee een horizontaal vlak gerealiseerd wordt.
Figuur 1.1: Opstelling met waterpasinstrument en baak.
In de figuur staat het instrument tussen twee punten A en B waarvan het hoogteverschil bepaald moet worden. In A en B worden latten met een cm-verdeling (baak) zuiver verticaal opgesteld; men kan de afstanden a en b op de baak aflezen en vindt:
hoogte B = hoogte A + a – b
Deze techniek noemen we de horizontale waterpassing van één slag. Hiermee kan het hoogteverschil tussen twee punten bepaald worden.
Indien zulke slagen achter elkaar herhaald worden, spreken we van een doorgaande waterpassing. Hiermee kunnen we de Z-coördinaat van een punt bepalen over een langere afstand.
Figuur 1.2: Doorgaande waterpassing.
In de figuur wordt de hoogte bepaald van punt RB20 vanaf de gekende hoogte in punt RB19.
We vinden:
H20 = H19 + ΣA – ΣV
Met:
- H19: De gekende hoogte van het startpunt
- H20: De gezochte hoogte van het eindpunt
- ΣA: De som van de lezingen op de achterbaken
- ΣV: De som van de lezingen op de voorbaken
Andere workshops:
Deze workshop focust op het gebruik van de theodoliet (of het totaalstation) als basisapparaat voor het inwinnen van meetdata en de verwerking van deze data tot een plan van de opgemeten omgeving.
Duurtijd: 3u
De theodoliet is het basisapparaat voor het topografisch werk en laat toe hoekmetingen in het horizontale en in het verticale vlak uit te voeren. Actueel zijn de meeste theodolieten uitgerust met een afstandmeter: deze toestellen worden door de term totaalstation aangeduid.
Door de evolutie van de theodoliet naar totaalstation en de ontwikkeling van landmeetkundige software werd het landmeetkundige rekenwerk vervangen door een geautomatiseerd proces. Landmeters beschikken vandaag over allerhande softwarepakketten om hun reken- en tekenwerk te vereenvoudigen.
Figuur 2.1: Opmetingen met het totaalstation worden verwerkt met landmeetkundige softwarepakketten.
De deelnemers gaan aan de slag met het totaalstation en verrichten de nodige opmetingen om nadien de meetdata te verwerken tot een plan. De uitgevoerde hoek- en afstandsmetingen laten toe om de drie dimensies van de gemeten punten te berekenen en een plan van de opgemeten omgeving uit te tekenen. Voor de verwerking van de meetdata tot een plan zullen we gebruik maken van landmeetkundige software.
Om tot een driedimensionale plaatsbepaling te komen, combineert het totaalstation twee meettechnieken die er samen voor zorgen dat van elk punt XYZ-coördinaten berekend kunnen worden.
1. De voerstraalmethode: de XY-coördinaten worden berekend op basis van de opgemeten horizontale hoeken en afstanden
2. De trigonometrische hoogtemeting: de Z-coördinaat volgt uit de combinatie van verticale hoekmeting en afstandsmeting.
Het principe van de voerstraalmethode komt op het volgende neer:
Op een bekend punt A als standplaats van het totaalstation meten we t.o.v. een ander bekend punt B elk detailpunt 1,2,… op met horizontale hoeken en afstanden. De gemeten hoekrichting en afstand worden samen de voerstraal genoemd. De verkregen waarden zijn de z.g. poolcoördinaten en kunnen omgerekend worden tot XY-coördinaten.
Figuur 2.2: Voerstaalmethode
Principe van de trigonometrische hoogtemeting:
In het verticale vlak kan met een totaalstation de elevatiehoek V gemeten worden, evenals de horizontale afstand HA of de schuine afstand SA.
Figuur 1.2: Totaalstation en principe van de trigonometrische hoogtemeting.
Hiermee kan het hoogteverschil dH tussen de theodoliet en het richtpunt berekend worden.
Indien ook de opstelhoogte van het instrument IH en de opstelhoogte van het richtpunt PH gekend zijn, dan is:
Zrpnt = Zstpl + IH + dH - PH
Met:
- Zrpnt: De gezochte terreinhoogte
- Zstpl: De gekende hoogte van de standplaats van het totaalstation
- IH: De opstelhoogte van het instrument
- dH: Het berekende hoogteverschil tussen het totaalstation en het richtpunt
- PH: De opstelhoogte van het richtpunt
Andere workshops:
Deze workshop focust op satellietplaatsbepaling - GNSS - en het gebruik van open geo-data.
Duurtijd: 3u
Landmeetkundige opmetingen worden bij voorkeur uitgevoerd in een nationaal stelsel.
Voor België betekent dit dat de planimetrische coördinaten (X-Y) van de opgemeten punten bepaald worden in het Lambert ’72- of Lambert 2008-coördinatenstelsel.
Met behulp van GNSS-plaatsbepaling kunnen opmetingen op een efficiënte manier gekoppeld worden aan één van deze nationale referentiesystemen.
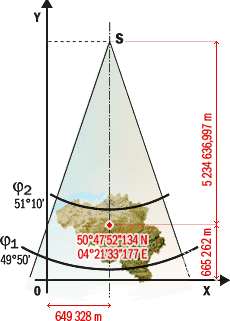
Lambert 2008
Figuur 3.1: Inmeten van referentiepunten met GNSS-plaatsbepaling.
Eén van de vele voordelen van deze koppeling is de uitwisselbaarheid van geo-data.
Dit maakt het voor landmeters bv. mogelijk om, bij de verwerking van hun meetgegevens, allerhande kaartmateriaal als achtergrond te importeren. Zo kunnen opmetingen en nieuwe projecten vanaf hun ontwerpfase gevisualiseerd worden in de bestaande omgeving.
Tijdens de workshop gaan we aan de slag met GNSS-instrumenten en zullen hiermee een basismeting verrichten in Lambert ’72-coördinaten.
Deze meetdata zullen we vervolgens importeren in een landmeetkundig softwarepakket.
Met de software zal dan de link gemaakt worden met allerlei open geo-data. Zo kunnen bv. orthofoto’s en/of het GRB (Grootschalig Referentiebestand) als achtergrond gelinkt worden.
Figuur 3.2: Open geo-data: orthofoto / GRB
Open geo-data biedt nog tal van andere toepassingen.
Bv. We zullen gebruik maken van LIDAR-data (open geo-data van de Vlaamse overheid). Met deze LIDAR-puntenwolken zullen we een digitaal terreinmodel (DTM) creëren om zo een virtuele 3D-voorstelling te genereren van het terrein.
Figuur 3.3: Ontwerp van een dijklichaam op basis van LIDAR-data
Andere workshops:
Duurtijd: 3u
Tijdens de workshop maken de leerlingen kennis met een drone (zelf vliegen laat de wetgeving in België in openlucht niet toe). Na een kleine demo met de drone en introductie in de wereld en principes van de fotogrammetrie gaan de leerlingen zelf aan de slag met terrestrische fotogrammetrie.
We nemen enkele (klas)foto’s met een gewone camera, meten enkele grondcontrolepunten in met een totaalstation en creëren een 3D-puntenwolk van de genomen (klas)foto’s. Om de omzetting te maken van 2D naar 3D maken de leerlingen gebruik van de software Pix4D. Aan het einde van de workshop gaan de leerlingen naar huis met een 3D-puntenwolk van de foto’s die met de groep werden genomen.
